One-color PINEM of a single VO₂ NW

First, we performed a one-color PINEM experiment on a single VO₂ NW to characterize the features of its PINEM spectrum at both insulating and metallic phases. The single-crystal VO₂ NWs were synthesized by chemical vapor deposition (see “Methods” section) and were directly transferred to an amorphous silicon nitride membrane (Si₃N_4, 20-nm thick) window for measurements. The left panel of Fig. 2a shows a bright-field image of the NW (diameter of ~350 nm). In this experiment, only the first optical pulse P1 (duration of 50 fs, λ = 800 m, fluence of ~4.1 mJ/cm²) was used to excite the sample with a polarization perpendicular to the NW axis to maximize the near-field excitation. Electron energy spectra were measured as a function of time delay (t₁) between the optical pulse P1 and the electron pulse (Fig. 1a). The recorded PINEM spectra are presented in Fig. 1c. Discrete peaks at integer multiples of \(\hbar \omega\) appear on both sides of the ZLP (the latter is shown as a shaded area in Fig. 1b at t₁ = 1.0 ps and −1.0 ps), and exhibit a maximum intensity at t₁ = 0 fs (the shaded pink curve). As the P1 optical pulse is much shorter than the electron pulse, the temporal profile of the PINEM intensity shown in Fig. 1d is mainly determined by the electron pulse duration (~650 fs via a Gaussian fitting), which represents the typical temporal resolution of regular UEM experiments. As a result of the “photon gating” in a two-color PINEM experiment, the temporal duration of the inelastically scattered electrons (PINEM electrons) is instead on the order of ~50 fs (given by the gating optical pulse duration^19,32), thus improving the temporal resolution of about one order of magnitude.

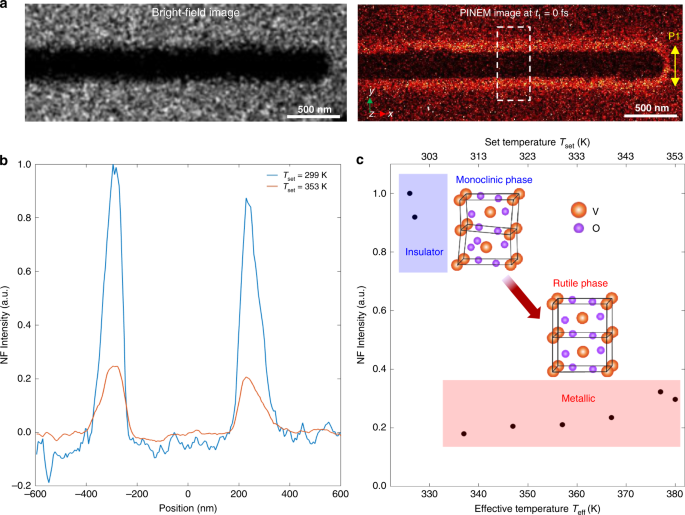
a Left panel: bright-field image; right panels: typical energy-filtered PINEM image (t₁ = 0 fs) of the investigated VO₂ NW (~350 nm in diameter) with the P1 optical pulse polarized perpendicularly to the NW axis. b Spatial distribution of the PINEM signal across the NW at T_set = 299 K (blue line, below transition) and T_set = 353 K (orange line, above transition). The intensity was integrated along the NW axis in the area indicated by the dashed white box in the PINEM image shown in the middle panel of a. The middle plane of the NW along the y direction is defined as zero for the positions in the horizontal axis. For this one-color PINEM measurement, 800 nm optical pulses (fluence of ~4.1 mJ/cm²) were used and the time delay was set at t₁ = 0 fs to maximize the PINEM coupling. c Integrated PINEM intensity of the NW as a function of temperature. T_set is the set temperature of the sample on the heating holder, and T_eff is the effective temperature, which differs from the T_set due to an additional temperature jump (~31 K) induced by the 800 nm optical pulse (P1). The PINEM intensity in the vicinity of the VO₂ NW significantly decreases when raising the temperature above the transition point (~340 K). The insets show the lattice structures of insulating monoclinic phase and metallic rutile phase, respectively.

To quantitatively characterize the localized near-field and the dielectric function of the VO₂ NW in insulating and metallic phases, we acquired energy-filtered images while thermally heating the sample across the IMT. A real-space map of the localized near-field is retrieved by selecting only those electrons that have acquired photon energy quanta (see “Methods” section). In these measurements, the time delay between the P1 optical pulse and the electron pulse is fixed at t₁ = 0 fs to attain the maximum electron–photon coupling. Typical room temperature bright-field image (left panel) and energy-filtered PINEM image (right panel) are shown in Fig. 2a. The optically induced near-field appears as a bright-contrast region surrounding the VO₂ NW. The maximum PINEM coupling at t₁ = 0 fs can be also clearly verified by the temporal dependent PINEM images in Movie S1. Figure 2b shows two typical spatial distributions of the PINEM intensity across the NW (obtained by integration along the NW axis in the dashed white box indicated in the right panel of Fig. 2a) at two different set temperatures, T_set = 299 K (blue line) and 353 K (orange line), respectively. Note that the optical pulse P1 also induces an additional temperature jump on the NW (~31 K, see “Methods” section), and thus the corresponding effective temperatures are 330 K (below IMT) and 384 K (above IMT), respectively. As shown in Fig. 2b, when thermally heating the nanowire across the IMT temperature (340 K), the PINEM intensity shows a pronounced decrease. This effect is further supported in Fig. 2c, which depicts the temperature dependence of the integrated intensity. An abrupt drop is observed when crossing the transition temperature, where the NW transforms from the monoclinic insulating phase into the rutile metallic phase (see insets in Fig. 2c). Such behavior can be attributed to the sudden decrease of the VO₂ dielectric function at the photon energy 1.55 eV⁴³, typical of a first-order transition from the insulating to the metallic phase, which results in a substantially smaller susceptibility. Such weaker dielectric response is thus responsible for a weaker localized near-field, and thus a reduced PINEM coupling.

To further confirm the dielectric origin of the observed behavior, we have performed numerical simulations using a finite element method, where we calculate the scattered field from a single VO₂ NW illuminated by an 800-nm optical field (see “Methods” section). In the calculations, the incident field is chosen to be linearly polarized along the y-axis (perpendicular to the NW axis) and propagating along z negative direction (Fig. 3a). The transition is modeled as a variation of the dielectric function from ε_ins = 5.68 − i3.59 (ñ_ins = 2.49 + i0.72) in the insulating phase to ε_met = 2.38 − i3.26 (ñ_met = 1.79 + i0.91) for the metallic phase as derived from ref. ⁴³ for the case of a thin film. In our experiment, we consider that the dielectric function of a thin film might represent a good approximation of the dielectric environment of our VO2 NWs, whose dielectric properties do not significantly differ from those of the bulk or high-quality thin films, especially for optical wavelengths in the visible range as adopted in our experiment⁴⁴. The dielectric permittivity of the Si₃N₄ substrate is kept constant⁴⁵. Also, all plasmonic effects for the investigated VO₂ nanowires are intrinsically taken into account within the finite element simulations.

Figure 3b represents the computed spatial distribution of the field integral β projected on the NW plane (xy plane) for the insulating and metallic cases, together with their difference map. In Fig. 3c, we plot instead the absolute value of β for the two phases integrated along the x-direction and shown as a function of the spatial y-coordinate across the NW. The simulations clearly confirm that the reduced permittivity in the metallic phase is responsible for a weaker scattered field at the NW/vacuum interface, which results in the lower intensity of the PINEM signal as observed in our one-color experiment (Fig. 2b, c).

Such pronounced contrast in the PINEM signal and the qualitative agreement between experiments and simulations attest to the sensitivity of our approach to probe modifications of the dielectric function crossing the IMT and thus the ability to monitor its ultrafast dynamics with a two-color PINEM approach. Such high sensitivity of the technique is obviously not limited to the 800-nm light used here, but it extends to a wide range of light wavelengths.

Two-color PINEM of a single VO₂ NW

We present here the two-color PINEM experiment performed on a single VO₂ NW. As we will describe below, such a method allowed us to monitor the transient change of the dielectric function of the NW accessing the IMT dynamics with combined fs and nm resolutions. For a conceptually clean experiment (Fig. 1a), two essential requirements need to be fulfilled: (i) the pump optical pulse P2 driving the Mott transition must photo-excite the VO₂ NW into the metallic phase without producing any appreciable near-field (i.e., PINEM signal), and (ii) the optical gating pulse P1 must have sufficient fluence to produce PINEM with an intense near-field signal but be below the threshold to trigger the Mott transition. In our case, an optical pulse (P2) with a central wavelength of 400 nm (duration of 50 fs) drives the transition, at which VO₂ exhibits a significant optical absorption. This P2 optical pulse was set at a fluence of ~15.3 mJ/cm² and was characterized by a polarization parallel to the NW axis, which minimizes the near-field excitation as the near-field only occurs at the end of the NW in such configuration (see the right panel of Fig. 2a). For the PINEM probe, the electron pulse was spatiotemporally coincident with a low fluence (~4.1 mJ/cm²) gating optical pulse (P1) with a central wavelength of 800 nm (duration of 50 fs). This P1 optical pulse was polarized along the direction perpendicular to the NW axis to maximize the optically induced near-field, and its time delay relative to the electron pulse was fixed at t₁ = 0 fs to maximize the PINEM coupling (see Movie S1).

In VO₂, a density-driven photoinduced IMT has been proven to occur with a critical energy dose ΔH_C of 2 eV/nm^3,46. For the case of a NW, the optical energy densities injected by the P1 and P2 pulses can be evaluated by resorting to scattering theory. In such framework, we determined the absorption cross section, C_abs, for the case of an infinite cylinder (see “Methods” section). The evaluated cross section is 2.63 × 10⁻⁷ m in the case of 400 nm (P2), while at 800 nm (P1) C_abs is 3.06 × 10⁻⁷ m. We then computed the absorbed optical energy density (energy per unit volume) injected within the NW as:

where ϕ_inc is the incident fluence and a is the cylinder radius. By considering the experimentally adopted parameters and geometrical configurations, we found that ρ_E,ph is about 1 eV/nm³ at 800 nm, while increases to 3.5 eV/nm³ at 400 nm. The fact that ρ_E,ph for 800 nm excitation is well below the critical energy dose ΔH_C, whereas ρ_E,ph for 400 nm is well above, is a strong confirmation that P2 is able to trigger the ultrafast IMT while P1 acts only as PINEM probe. Note that, electron beam may also induce effects on the IMT in VO₂, such as lowering the IMT temperature by creating oxygen vacancies⁴⁷. However, the dose of the electron pulse in our experiment is several orders of magnitude smaller than the conventional thermal electron beam and its effect is negligible.

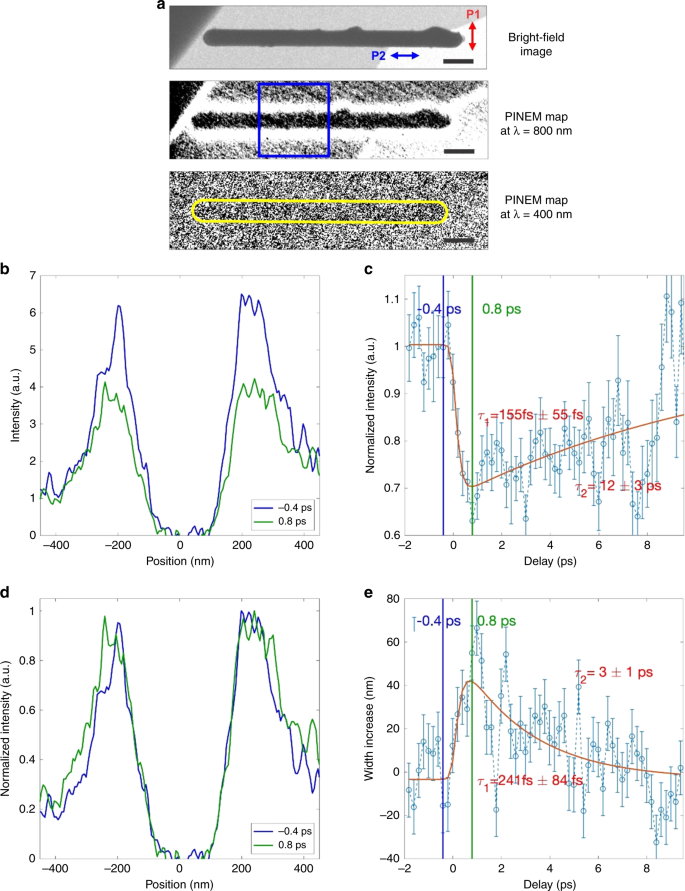
As mentioned above, the amplitude of the localized near-field created around the NW by the P1 optical pulse (800 nm) strongly depends on the susceptibility and thus on ε(ω). Besides the amplitude, also the decay length of such near-field can be directly connected to the material permittivity. In fact, according to Mie scattering theory for an infinite long cylinder the complex refractive index exhibits a direct spatial dependence⁴⁸. This means that a change in the dielectric response induced by the P2 optical pulse (400 nm) can lead both to a modification of the PINEM intensity and, at the same time, to a different decay length of the PINEM signal at the NW/vacuum interface. To combine spatial and spectroscopic information, we acquired energy-filtered PINEM images at different delay times of t₂ (see “Methods” section). Figure 4a shows the bright-field image of the investigated VO₂ NW sitting on the Si₃N₄ membrane (left panel), and one of its corresponding energy-filtered PINEM image (t₁ = 0 ps, t₂ = 0 ps) (right panel), in which the transient near-field appears as a bright-contrast region surrounding it. To quantify the dielectric response to the IMT, we integrated the PINEM signal along the NW axis (within the area indicated by the blue box in the right panel of Fig. 4a) and plotted it as a function of the position across the NW. Typical plots of such spatial distribution are shown in Fig. 4b for two different delay times, t₂ = 0 ps and t₂ = 1.28 ps (t₁ = 0 ps). For a more clear comparison of their lateral decay length, we also plot them in Fig. 4c with each curve normalized to its own maximum. The PINEM intensity shows a substantial decrease at 1.28 ps, while the lateral decay length shows a simultaneous increase. The variation of the integrated PINEM intensity as a function of the delay time t₂ is plotted in Fig. 4d. Upon the 400 nm pump, the PINEM intensity shows an initial ultrafast decrease of ~30% with a time constant of ~145 fs, followed by a slower recovery on tens of ps timescale. Such behavior is consistent with a transformation to a metallic phase with a smaller permittivity, which results in a weaker PINEM coupling (consistently with the observations of one-color PINEM at high temperatures). Figure 4e shows the temporal evolution of the lateral width (measured as the full width at half maximum, FWHM) of the integrated PINEM signal surrounding the NW. We observed an ultrafast lateral increase of the localized near-field profile of about 40–60 nm with a time constant of ~155 fs, followed by a slower recovery on a ~10 ps timescale, whose dynamics is consistent with the intensity variation. Therefore, using our approach, it is also possible to follow the transition by looking at the change of the nanoscale spatial decay of the localized near-field. In both Fig. 4d, e, the red curves represent the best fit of the experimental data with a biexponential model where the temporal duration of the gated PINEM electrons and pump optical pulse P2 is explicitly taken into account. Importantly, it is also worth noting that the observed experimental behavior is well confirmed by the numerical simulations obtained for the two phases (see Fig. 2b), which show a lower interaction strength and a longer spatial decay in the metallic case with respect to the initial insulating state (see Fig. 3c).

a Bright-field (top panel) and energy-filtered PINEM images measured at a pump wavelength of 800 nm (middle panel, t₁ = 0 ps) and at 400 nm (bottom panel, t₂ = 0 ps) of the investigated VO₂ NW (~350 nm in diameter) on the Si₃N₄ substrate. The red and blue arrows in the top panel show the polarization directions of P1 and P2 optical pulses, respectively. The blue box in the middle panel indicates the area along the NW where the PINEM signal is integrated. The scale bars are 500 nm. b Spatial distribution of the PINEM signal across the NW showed at the zero delay time t₂ = 0 ps (coincidence between pump and probe, blue curve) and 1.28 ps (green curve), respectively. c Normalized spatial distribution of the PINEM signal across the NW showed at the zero delay time t₂ = 0 ps (blue curve) and 1.28 ps (green curve), respectively. Both curves are normalized to their own maximum intensity. d Spatially integrated PINEM intensity as a function of delay time (t₂) between the 400 nm pump and the PINEM probe (open circles); the red curve is the best fit of the experimental data with a biexponential model convoluted with time-resolution of the technique. e Temporal dependence of the lateral spatial decay (measured at full width at half maximum) of the PINEM signal surrounding the NW. The red curve is the fit with two timescales convoluted with time-resolution of the technique. The error bars have been obtained by considering the measurement uncertainty and the variance within the counts.

Microscopic mechanism for the IMT dynamics

At a microscopic level, the Mott transition of bulk VO₂ from the monoclinic insulating phase to the rutile metallic phase proceeds through a series of transient steps characterized by a well-defined character and time constants⁴⁹. The photoexcitation of the insulating phase corresponds to a photo-doping of the conduction band with excited electrons^50,51, and thus induces a redistribution of the electronic population within the 3d-symmetry bands. Such electronic rearrangement is thus responsible for a bandgap renormalization, which leads to an instantaneous collapse of the insulating bandgap (0.7 eV), rendering VO₂ metallic⁵⁰. At the same time, the depopulation of bonding V-V orbitals is responsible for a strong modification of the double-well interatomic potential of the monoclinic lattice, which becomes highly anharmonic and flat. Ultrafast optical probes, which are particularly sensitive to the dielectric environment, have shown that such lattice potential change, which is related to a modified screening of the Coulomb interaction, occurs with a sub-100 fs time constant in bulk VO₂. At this point, the presence of a flat, anharmonic single-well potential triggers the atomic motions and leads to a removal of the long-range Peierls V-V dimerization. This has been observed with ultrafast structural probes to evolve on a 300–500 fs timescale^6,7,10. Recently, large-amplitude uncorrelated atomic motions have also been noted to play a role in the V-V bond dilation on a timescale of about 150 fs⁷. Finally, the thermalization of the electronic population mediated by the excitation of transverse acoustic phonons over several ps temporal range can drive the lattice toward the final rutile metallic phase^9,10,49,51.

As shown in Fig. 4b, d, the localized PINEM signal from the VO₂ NW observed in our experiments exhibits an initial ultrafast dynamical process with a time constant of ~150 fs followed by a slower recovery process, which indicates the transition from the insulating to metallic phase without evidence of passing through any intermediate states. Furthermore, this value is nearly twice shorter than the ~300 fs of the coherent V-V displacement motions observed from previous structural probes^9,10, while it is consistent with the timescale for photo-doping-induced lattice potential change, which could abruptly unlock the V dimers and yield large-amplitude uncorrelated motions, as also observed from the ultrafast optical studies on the bulk crystals⁷. Thus, with our approach, we could capture the transient state in which the NW has become metallic as induced by the photocarrier-induced change of the interatomic potential, but before the crystalline lattice perturbations occur and so the structure remains in the monoclinic phase, namely, the transient quasi-rutile metallic phase⁷. Since both the PINEM intensity and its spatial distribution can be directly related to the dielectric function, our method is inherently sensitive to the electronic dynamics of the VO₂ NW. The advantage of our approach is the ability to retrieve such electronic dynamic information on a single nanostructure with combined nm–fs spatiotemporal resolution, which is particularly relevant, especially when nanoscale inhomogeneity plays a decisive role in the transition process¹⁸. Following the fs dynamics, we also observe a slower recovery toward the electronic equilibrium through the electron–lattice coupling on a timescale of tens of ps, which can be readily associated with anharmonic excitations of acoustic phonons. Thus, a themodynamically stable metallic rutile phase is not fully reached and then the system relaxes back to the insulating monoclinic phase.

It is worth noting that, because the photon-pump/PINEM-probe experiment was carried out in an ultrafast electron microscope, it would be possible to interrogate similar nanostructured materials under the same experimental conditions by ultrafast dark-field imaging or ultrafast diffraction using the temporally gated PINEM electrons. The latter would provide structural information with similar enhanced temporal and spatial resolutions and enable the possibility to simultaneously explore both the electronic (dielectric) and structural dynamics of the investigated individual nanostructures on a few tens of fs timescale.

In this work, we have implemented a two-color near-field UEM method and demonstrated its ability to access the initial ultrafast electronic process in the optically induced IMT in an individual VO₂ NW. We observed the temporal evolution of its dielectric response with PINEM imaging on nm and fs scales, achieving a combined spatiotemporal resolution several orders of magnitude larger than the conventional optical probes and static imaging. The high sensitivity of PINEM to the ultrafast dielectric response driven by laser photoexcitation attests to the high versatility of our approach for spatially resolved investigation of electronic dynamics and phase transitions that last a few tens of fs. Furthermore, incorporating with the advanced attosecond optical pulse generation techniques^32,52, it is feasible to achieve sub-fs and even attosecond temporal resolution in UEM via our approach. Therefore, this demonstration would be an important step towards the ultimate establishment of sub-fs/as resolution in electron microscopy for capturing electron motion in nanomaterials in real space and time.